Girls' participation and achievement in mathematics have become important issues in recent years, firstly in the United States in the 1960s and a decade later in the UK. Since that time much has been written on the subject and a number of theories proposed as to its nature and causes. Some of these will be reviewed in the course of this essay.
The purpose of this account is to explore to what extent the underlying philosophy of the UK National Numeracy Strategy (NNS) has been designed to, and succeeds in, addressing the issues of gender differences within mathematics learning for children at primary school age. Although the concern with girls' attitudes has focused on the secondary and tertiary phases of education, this study is concerned with the forming attitudes of Key Stage Two children. This is necessarily so because the NNS is, at present, a primary initiative. The Strategy has been in operation for a year now. To change attitudes, that over centuries have become part of a culture, will take time. Much of current primary classroom practice is modelled on teaching approaches outlined in recent government initiatives for English and mathematics. A key feature of these approaches is interactive teaching. This requires a micro-culture to be developed within the classroom in which children of both sexes and all abilities feel comfortable in exchanging their views and testing their ideas. Within mathematics this involves children explaining, exploring, hypothesising, predicting, testing and talking about their mathematics amongst themselves and with their teachers. Mistakes are treated as new discoveries and can be made with neither fear of reprimand nor of ridicule. Such an approach is moving towards the view of mathematics as fallible and accessible to all. The idea of mathematics as fallible will be raised later in this essay.
Much time and resource has been invested in the NNS, initially to address perceived shortcomings in mathematics teaching and learning at Primary level. Issues of gender differences are complex and extend beyond the confines of this or that syllabus. However, if the NNS initiative is able to promote mathematics that is as accessible to girls as it is to boys, not only in the styles of teaching it employs, but also through the development of teachers' own attitudes towards the subject, then a small step may have been taken towards addressing an underlying but important issue - that of girls' attitudes towards, and under participation in, mathematics. With this in mind, the aim of this study is to obtain the thoughts feelings and perceptions of a small group of ten and eleven year old children regarding the mathematics and mathematics teaching that they had experienced over the previous year.
Girls under participation in and attitude towards mathematics may be a problem older and more deeply rooted that we care to acknowledge. Harris (1997) argues that the problem is at least two thousand years old and probably older. Certainly within the history of Christian education, "…mathematics was always a gendered subject…"(p39) and that the Church authorities, whose schools offered what education was available, were "blatantly misogynist." (p26) She suggests that women have been socially conditioned over the centuries and that the result of this has been to create the belief that girls and women do not do mathematics because they cannot and that such a view remains strong in the perception of the public. Her case is substantiated with evidence from numerous sources. A Saturday review of the 1880s went further and denounced educated women as "defeminated, hermaphrodite, mongrel, specimen of vermin, one of the most intolerable monsters in creation" (p68), whilst elsewhere it was pronounced that, "Educating girls led to a moral decline of the family, indeed the race and empire." Against such a background it is not difficult to see why women have had a poor deal in terms of their schooling and over the years have had to press for what is theirs by right.
Running parallel with past attitudes towards the place of women in society and their rights to education, has been a view of mathematics itself, which has held sway since the time of Euclid and before, and has only in the twentieth century been brought into question. Ernest (1991) debates the existence of two opposing philosophies of mathematics. On the one hand is the traditional or absolutist view of mathematics which maintains that mathematical knowledge is made up of absolute truths and represents a sphere of certain knowledge. These truths, once established by cold reason alone, stand for ever within the domain of human consciousness. Indeed, the claim is that they were true before humans came to be and will remain so after our departure. The absolutist school goes on to argue that mathematical truths are thus timeless, value free and culture free. Such a view has, over the years, given grounds for mathematics to be viewed as cold, abstract, ultra rational and difficult, and more importantly, by association with other ideas and values, 'unfeminine.' Link this widely held view of mathematics with a perceived role of women as subordinate to men, which in some groups of society, is still embedded within the culture here, and certainly elsewhere, and the enormity of the problem begins to become apparent.
To counter this, a more recently presented Fallibilist view of mathematics has been suggested which claims that mathematics is fallible, laden with the values and culture of the society that created it and as such, should never be regarded as beyond revision and correction. The Fallibilist view of mathematics does not reject the idea of structure within mathematics. Rather it suggests a realm of multiple overlapping and evolving structures that can grow and develop, be modified, refined and redefined over time. Here is a new view of mathematics, a view encompassing warmth and humanistic traits, a view that admits to a process of investigation, blind alleys, restarts, mistakes, frustrations, confusions, failures and successes. Finally, all being well, a neatly packaged product is presented for consideration, a package that itself is open to scrutiny, refinement and correction, a package that is imbued with the values and cultures which contributed to its creation.
Not only is the nature of mathematics questioned. Walkerdine (1989) launches an attack on the research methods and conclusions drawn regarding girls' performance in mathematics, (eg Shuard, 1981, 1982) calling into question the reliance on statistical significance used by those researchers who concluded that girls performed better at tasks requiring only 'low level' or rote learning skills, thus negating the small measure of success found in girls' achievements. (p12) Also cited are examples of teacher attitude favouring boys' success over that of that girls'. (p11) Linked with this or as a consequence of it, there appears to be a tendency for boys to see their success in mathematics as attributable to ability, whilst girls regard it more as good luck. (Weiner 1971)
School mathematical texts too, have been the subject of scrutiny. Walkerdine (1989) draws on the research findings of Jean Northam (1983) who carried out an analysis of primary and secondary texts and concluded that, at the time of her writing, stereotypical styles of male/female roles in society were still apparent in the then currently used texts and could still be teased out from the more up to date versions of the late 1980s. These usually took the form of the girl being subordinate to the boy, either visually, or by implication within the text, or in one example cited, where girls only were featured, of having to ask the reader's advice on a course of action through solving a problem. (Walkerdine 1989, p193)
Walkerdine (1982) suggests that factors affecting girls' mathematical performance were also to do with the subject itself and the way it was taught. For example, her researchers from the Girls and Mathematics Unit noted that in early years, girls did enjoy playing with construction toys, an activity traditionally associated with boys, but that teachers assumed that girls would not want to continue with these pursuits, leading to a lack of encouragement and even a disregard of the activity when it did happen. She argues that gender differences have much to do with a myth regarding male superiority in mathematics. The myth is so embedded within, and colours the view of society, it came to be perceived as true. Walkerdine attributes no blame to groups or sectors of society but is more interested in identifying and rectifying the causes of the myth.
Biological differences have been examined in attempt to establish explanations for differences in mathematical performances between girls and boys. The effect of biological factors is not fully understood (Ernest 1996) and would not account for the differences in mathematical attainment being more dominant in some countries than in others. Burton (1986) and Walden and Walkerdine (1985) examined the issue of differences in spatial ability concluding respectively that only the top ten percent of the population showed a significant difference and that no firm judgement could be made. In an attempt to refocus on the under-participation of girls in mathematics post sixteen, Leone Burton (1986), drawing on a then recent publication by Chipman et al, (1985) identified the following factor relating to female participation in mathematics at secondary and tertiary level in the United States.
Teachers _ whose awareness of and sensitivity to the effects their behaviour on pupils appears to be crucial. Related to this is the kind of classroom environment which is fostered, the image conveyed of the nature of mathematics and the mathematical enquiry and the relationships which are developed between the teachers and the taught. (Burton 1986, p2)
Current styles of primary teaching lay stress on this aspect of primary classroom practice. The NNS requires of teachers that they "..ensure that all pupils take part..", that they promote learning by "…listening carefully to pupils' responses (to questions) and responding constructively…" and "…make sure that all pupils of all abilities are involved and contribute to discussions…" (NNS 1999, Section 1, p12). There is, within our culture, a social acceptability of being poor mathematically (Haylock 1995) and a readier acceptance of innumeracy than illiteracy. (OfSTED 1997). This document also argues that if children (of both sexes) become anxious about mathematics because of confused or confusing teaching, attitudes to mathematics can become and remain negative, with destructive consequences for future achievement and enjoyment. No mention here is made of gender differences because in terms of achievement at primary level there are none, but if the deeper issue of differential participation rates later on is to be addressed then the notion of mathematics as warm, value laden, fallible and feminine friendly needs to run as a golden thread through the developing tapestry of mathematical skills and concepts that is being woven.
In order to keep within the scope of this essay, it was decided to take account of only lower achieving pupils at upper Key Stage Two. Lower achieving children were selected for the study because it was considered that they would provide a more critical 'measure' of attitude toward the learning of mathematics, in that more able children - those already succeeding under the previous system of teaching - may have gained and retained positive feelings towards the subject. At the time of writing, the children interviewed for the study had had two years of 'Numeracy Hour' style teaching, while still being able to remember the teaching they experienced before the pilot scheme was introduced. A small study such as this with the limited approach employed can only investigate a tiny part of the issue as complex as the one the title suggests and no pretence is made here to do more than this. The children selected for the study had not been taught by me. This was done deliberately. I was aware that some children might make the kind of replies that they believed I wanted to hear. However, I thought these replies less likely from children that I had not taught, although I cannot rule out that this did not happen. Large scale interviewing was not possible as the number of potential participants was limited so I decided to base my enquiry on the case studies of a small number of children. There still remained a number of methodological issues to decide upon. How many children should I chose to interview? Since I was interested in girls' attitudes to mathematics, should I chose only girls? What form should the interviews take? Should I be a participant in the discussion of the issues that I wanted to raise or merely focus on asking questions and noting responses. It was possible that some of the lower ability children chosen would be less articulate and less inclined to be forthcoming in their responses. Accordingly, I decided to allow myself the freedom to ask follow up questions as required, in order to encourage the children to give their views as openly and as fully as possible. Because of the limitations of time (it was near to the end of term and some of the children that I wanted to interview would leave the school in July) I decided to interview just ten children, five boys and five girls. Boys were included in the sample to provide a comparison in terms of pupil response. In the event I was only able to speak to six children - three girls and three boys. The children were selected for me by their teacher from a lower ability group. I decided to use a semi-structured interview format, using a questionnaire as a framework for my questions. Within the questionnaire itself, I wanted to focus on both the style of teaching of the mathematics lessons and, to some extent, the content of that which was being taught. The questions asked focused on these aspects and were designed in an attempt to discover, within the sample, whether the approach of the NNS was motivating, and if so, was it as motivating to the girls interviewed as it was to the boys. I was aware that I could set out with an expectation of positive feelings and designed the questionnaire to avoid, as far as was possible, leading questions. Nevertheless, my purpose was to see, if from the small sample of children interviewed, attitudes to mathematics were generally positive or negative and if the former, was there anything to suggest that it was because of the way the subject was being taught. From such a small sample, I would not be able to make any generalisations, but merely to gain insight into some of the thoughts and feelings of those children interviewed regarding their mathematics. The children's responses might indicate some gender differences.
The children were interviewed individually, in either the school library or the music room. Both were settings that were familiar to the children and presented atmospheres in which they could feel relaxed. I asked each child if s/he minded the interview being taped. None objected and I recorded some of the interviews using a micro-cassette recorder. As a back up, I made notes on each child's responses as we progressed. The back up notes proved essential as due to some technical difficulties, only two of the recordings were usable. A blank questionnaire is shown in the appendix.
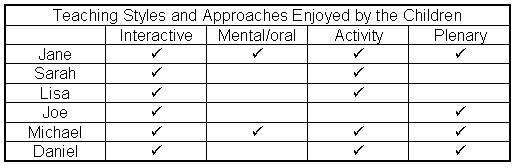
Jane (a pseudonym as are all names given below) is a hard working girl of eleven years. She pursues a number of interests outside school and her parents have high expectations for her. She is a sociable child with a circle of close friends. According to her teacher, Jane had recently moved from a lower to an upper English set through gritted determination and hard work. She began by telling me that she "..was no good at maths" and then spoke with considerable enthusiasm about mathematics for the whole interview. She enjoyed the mental starter sessions, saying that she knew her tables which helped a lot. She felt that the daily practice was helping her to get better at working things out in her head. She thought her confidence had grown. This was exemplified when she told me that she was prepared to try different ways of working something out until she got the "right answer."
Jane enjoyed the practical activities most and especially those which involved collaborative work. If she could work with others then she enjoyed problem solving too, even if the problems were hard. She enjoyed the interactive parts of the lessons, saying that it was useful to be given the opportunity to explain her thinking and to hear the ideas of other children as well as those of her teacher. Jane was hesitant about new mathematical ideas, but admitted that they "grow on you."
Jane was possibly the most positive of the children interviewed highlighting several areas of the NNS approach which pleased her, notably the interactive and collaborative nature of much of the work.
The first boy I spoke to was Joe, aged ten years. Joe is a child of average ability generally, above so in art, who nevertheless performs at a level below that which would be expected for him in all other subjects. According to his teacher, this is partly because of various circumstances relating to his background. He was excited about the prospect of being interviewed but found it difficult to express his views clearly. In response to a question about some mathematics that he had enjoyed recently, he mentioned games which are sometimes played to consolidate previous learning. 'Games' is an area where it is possible to make mistakes - get things wrong without social stigma. This is important to Joe who constantly requires approval from peers and adults. When asked about mathematics he disliked he answered 'decimals' and later, 'data handling', but was unable to be precise about his reasons. Later, when I asked Joe about the parts of the lessons he enjoyed most he replied the activity session (his words) and the plenary. (not his word) Regarding the plenary, he explained as follows:
Interviewer: What do you find helpful about the end session?
(Joe had already indicated that he found it helpful)Joe: I think…um…when we come out with our answers and our ideas.
Interviewer: How does it help you?
Joe: It sort of puts new ideas into your head and old ideas into your head and it gives you the answer to, say maybe a really hard question.
Interviewer: Something you'd been stuck on earlier.
Joe Yes.
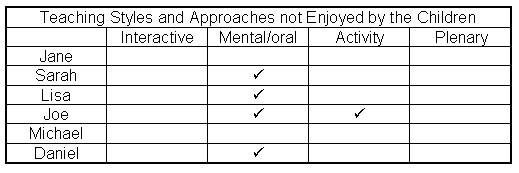
Joe clearly found the interactive nature of this part of the lesson helpful. A key element in the teaching of mathematics today involves the teaching of mental strategies. When I asked Joe if he liked this part of the lesson, he told me he did not know his tables well and so could not do parts of the session. He did not believe he was getting any better at working things out in his head despite daily practice. He found it much easier to work things out on paper. "It's much easier because you can use the paper for your sum…and working out." Joe was not confident with number and preferred the set algorithms that he had been taught in earlier years. On the subject of group work, Joe said that he liked to work alone because he was "less distracted."
Despite his limited ability with the subject, Joe showed a generally positive outlook towards his learning in mathematics.
Sarah's teacher told me that she has limited literacy and numeracy skills. She finds it difficult to remember her tables and does not enjoy any form of calculation work. Sarah was unable to articulate her feelings to any great extent but did indicate that she found mathematics lessons enjoyable, especially practical work and activities involving shape and space. She does not enjoy mental arithmetic particularly with harder numbers. She offered eleven plus twelve as an example involving harder numbers. I asked her if she would work it out for me there and then and she did using a near doubles strategy. I suspect that Sarah lacks confidence and can possibly do more than she thinks. She thought that she was improving with mental arithmetic and was able to do seven plus eight using the same near doubling strategy. She sometimes finds it hard to remember how to work things out but was unable to give me an example.
Although apparently of very limited skill, Sarah's responses suggested that she was comfortable with her performance in mathematics and did not feel pressured in any way.
Michael is eleven years old. According to his teacher, he has poor literary skills but had worked extremely hard over the previous two years to improve them. He also worked hard at his mathematics and spoke with confidence about what he had done. Michael told me that he "quite liked" the warm up part of the lessons because he enjoys finding the answers to questions using the digit cards. He gave as an example ten times five to which he knew the answer, but admitted that he was not comfortable with multiplication generally. He thought that he was getting quicker at working things out in his head and that the daily practice was useful. Because of his reasonable success rate he did not feel under pressure or embarrassed at being asked to display his knowledge in the semi-public arena of the mental-oral session.
Michael told me that he did not usually forget how to work things out (algorithms) but later changed his mind, saying that he would sometimes use his own methods. He thought his "own methods" often preferable because "others can't copy." In the interactive part of the lessons he said that he became confused sometimes and needed a while to "find out how to do it." Occasionally he would "go back to grandad's method."
As with the other children, Michael enjoys the practical activities and described
one in which his group had been asked to measure the corridor. They repeated
the measurement several times and arrived at different answers; twenty nine
or thirty metres. They eventually agreed that their best answer was twenty nine
metres because after repeating the activity that was the result that came up
most often.
Michael prefers to work in a group because he thinks discussion is important.
"People who don't know can catch up in discussion." He finds the plenary
sessions useful and likes to contribute if he knows what he is talking about.
Michael is a reflective boy, aware that others are sometimes quicker at grasping new concepts, but nevertheless content with his own learning style and the progress that he is making.
Daniel enjoys mathematics lessons and began by describing to me a challenging investigation that he was working on which involved frogs leaping on to lily pads. He likes the interactive parts of the lessons because it is "good to hear what others are saying." Sharing thoughts with the class helped if there was something that he did not know. "Sometimes others can explain."
Daniel enjoys the structures of the lessons apart from mental arithmetic. He is beginning to develop strategies for coping with mental work but has not completely formed them in his mind.
Interviewer: Can you work out 24 X 7?
Daniel: It's 2 x 7 ……… times by 10 then add 4……
Daniel was unsure about his answer. He knew he had not got the right answer but could not explain why. Daniel concluded that he sometimes enjoyed the lessons; it depended on the day. According to his teacher, Daniel is prone to violent mood swings and bouts of apparent tiredness and on bad days finds it difficult to cope.
Lisa is a sociable ten year old who recently joined the school. She is popular with the other girls in the class and quickly formed a close circle of friends. She enjoys participating in teaching and activity sections of the lessons, but does not find plenaries useful. She was strong in her criticism, saying that she "hates them because it's embarrassing when you get it wrong." Lisa dislikes the mental arithmetic sessions and feels tense and pressured partly because she is unsure of her tables. She told me that she becomes confused with mental methods, much preferring to use standard written algorithms to calculate. The daily mental practice was not helping her to improve, rather the reverse, in that she felt that she was getting worse.
Lisa: When I've done it once, if it's right I usually get it wrong later.
Interviewer: Why?
Lisa: I forget what I've done.
Interviewer: Do you need more practice?
Lisa: I do practise.
Lisa spoke forcibly and with a hint of anger at this point. Despite her sociable nature, she prefers to work alone, feeling pressured at the possibility of being left behind in a group situation. Lisa told me that she did not like mathematics; that she did not like working with numbers.
Conclusion
All of the children interviewed, with the exception of Lisa, spoke positively about their mathematics. Even those for whom the subject presented considerable difficulties enjoyed the lessons and participated in class and group work to a greater or lesser extent. They indicated that they enjoyed particular sections of the structured lessons and that plenaries sometimes helped them to understand concepts that had eluded them earlier. The children enjoyed practical activities and with the exception of Lisa and Joe, group work. It was not clear as to whether the NNS had had any impact on gender differences within the sample. Jane believes that she is poor at maths, yet is motivated to work hard and spoke positively about all aspects of the teaching. Lisa, possibly the more outspoken of the two, also works hard but expressed some dislike for the subject. Sarah, the least able of the trio of girls interviewed, had mostly positive comments and was pleased to be able to demonstrate some of the mental arithmetic skills that she had acquired through the NNS teaching approach, despite saying that she disliked mental calculation. Jane was the only child who said that she liked the mental oral starter session mainly because "I know my tables." For the rest, who did not enjoy this part of the lesson, the reason most often given was that they did not know their tables well. Mental/oral starter sessions take a variety of forms and a direct knowledge of tables is sometimes helpful but not always needed. Yet, the only child who felt comfortable with this part of the lesson was one who knew her tables. The interactive teaching and activity parts of the lessons were enjoyed by all the children, while Jane, Daniel, Joe and Michael thought that the reviewing and sharing of ideas in plenary sessions was useful.
The impact of a study such as this is limited by its scope and methodology.
The number of children interviewed was extremely small and the interviewing
procedure itself was in some respects unsatisfactory. The questionnaire tried
to address two issues: teaching styles and teaching content. Early in the study,
I believed that both these strands should be addressed, but later realised that
in attempting to so I may have clouded some of the very issues that I wanted
to explore. Consequently, not all the information from the questionnaire provided
new and useful material for the study, raising questions of validity. A quantitative
approach focusing on the way that mathematics is taught through the NNS might
prove to be a more reliable indicator of attitudes and if they exist, gender
trends. Over this small group of case studies, no suggestion of pattern began
to emerge regarding the children's attitudes to the different parts of the lessons.
All enjoyed at least one aspect of the teaching approach, and most disliked
one or more sections of the lessons. Nor was there any discernible indication
of gender trends. The NNS as an approach to teaching mathematics to Primary
age children is still in its infancy. Studies carried out before the implementation
of the framework provided evidence to support the assertion that the teaching
methods employed were successful in raising standards of achievement at all
levels, but particularly in lower ability children. The intention was to address
the issue of attainment and not attitude. The former can be viewed as relatively
short term and is easy to measure; the latter may form and reform over a longer
period of time. At this stage the question of the impact, if any, of the structures
and teaching styles embedded within the NNS on gender issues remains open.
Bell, J. (1995) Doing Your Research Project. Buckingham Philadelphia: Open University Press
Burton, L. (1986) Girls into Maths Can Go. London: Holt, Rinehart and Winston.
Chipman, S.F. Brush, L.R. and Wilson, D.M. (1985) Women and mathematics: Balancing the Equation. Hillsdale, NJ and London: Lawrence Erlbaum Assoc.
Cohen, L and Manion, L (1994) Research methods in Education. London: Routledge
Department for Education and Employment (1999) The National Numeracy Strategy. Cambridge university Press
Ernest, P. (1991) The Philosophy of Mathematics Education. Basingstoke: The Falmer Press
Ernest, P. (1994) The Nature of Mathematics and Equal Opportunities. University of Exeter
Fraser, H. and Honeyford, G. (2000) Children, Parents and Teachers Enjoying Numeracy. London: David Fulton
Harris, M. (1997) Common Threads. Trentham Books Ltd; England
Haylock, D. (1995) Mathematics Explained for Primary Teachers. London: Paul Chapman Publishing.
Hughes, M, Wikeley, F and Nash, T. (1994) Parents and their Children's Schools. Blackwell: Oxford.
OFSTED (1997) The Teaching of Number in Three Inner-urban LEAs, reference:115/97/DS. London: OFSTED.
Walkerdine, V. (1989) Counting Girls Out. Virago: London
Weiner, B. (1971) Perceiving the Causes of Success and Failure. New York: General Learning Press