Judith C. Rowe
11 South Avenue
Littleover
Derby DE23 6BA
AN EXPERIMENT IN THE USE OF GAMES IN THE TEACHING OF MENTAL ARITHMETIC
INTRODUCTION
Following a voluntary pilot test in 1997, a statutory mental arithmetic test
was introduced into the Key Stage 3 SATS examinations during 1998 for all pupils
in England and Wales working at National Curriculum level three or above. This
examination had a weighting of twenty percent. Although there are concerns about
various aspects of these mental arithmetic tests they are to continue, in more
or less the same form, for 1999.
I currently teach a year nine group of middle to low attainers in mathematics and have been concerned about their preparation for this mental arithmetic test. Throughout the academic year we have spent time each week on mental arithmetic, but generally in the form of a short test. Initially this seemed beneficial but as time has passed it seems to have polarised the group into those who enjoy mental arithmetic and are keen to do well and those who struggle with it and have not been motivated by the test situation. I was therefore keen to try a new approach, and decided that using games would be a contrast to the approach I had used so far. I decided to focus on one particular topic, and this was the relationships between fractions, decimals and percentages and the use of them in simple calculations. I used a simple diagnostic test at both the start and the conclusion of the experiment to evaluate the effectiveness of the two games that I had chosen to use with the class.
I will start by briefly looking at the research on the difficulties children encounter with relationships between fractions, decimals and percentages and then move onto research that has been conducted into the use of games in the classroom and in particular their use for mental arithmetic. The results of the experiment are presented next. I will finish with a summary of the results and their significance together with my personal reflections on the experiment.
REVIEW OF LITERATURE
What are the problems with decimals, fractions and percentages?
The problems my class have had with fractions, decimals and percentages are
nothing new. Other studies have recognised the problems children have with these
topics, and I quote here examples from two such studies. The results of the
sixth National Assessment of Educational Progress (NAEP) conducted in 1992 highlighted
the difficulties students have in tasks that have mixed fraction and decimal
notation. One particular item illustrates this clearly:
Of the following, which is closest in value to 0.52?
![]()
Only 51% of eighth grade students (13 years old) chose 1/2 as the fraction closest to 0.52, with 29% thinking that 1/50 was closest. The authors felt that the particularly low performance on this task was due to difficulties students have in tasks that have mixed fraction and decimal notation. These two items from the Concepts in Secondary Mathematics and Science (CSMS) study reported in Hart (1981) highlight two other problems in this area.

Hart and the CSMS team (1981) noted
It is above all clear that the learning of whole numbers and decimals is not
just a matter of recalling some place-names and a few rules of computation,
as it appears to be from the textbooks. ...
Instead, it involves internalising a whole chain of relationships and connections,
some within the place structure itself (e.g. 0.9 is equivalent to 0.90) some
linking to other concepts like those of fractions (e.g. the notion of one
hundredth and its relationship to one tenth), some visual correspondences
and some connecting applications to the real world. (page 64)
Having recognised that these problems are widespread I now consider the advantages
and disadvantages of using games to help my class cope with these topics in
mental arithmetic tests.
What is a game?
There are differing definitions of mathematical games in the literature. In
the context of this experiment I will use the definition offered by Ainley (1988),
The most effective mathematical games are those in which the structure and
rules of the game are based on mathematical ideas, and where winning the
game is directly related to understanding this mathematics. (page 241)
Why play games?
Hatch (1998b) classifies the intrinsic advantages of games under three headings:
1. Learning
2. Ways of working
3. Pupil experience
and I will use her structure to examine the literature available on games.
1. Learning
Much of mathematics teaching revolves around giving children practice in newly
acquired skills and of reinforcing and developing skills. Games provide a way
of taking the drudgery out of the practice of skills, and indeed of making the
practice more effective. Hatch points out that 'a game can generate an unreasonable
amount of practice' (page 3). A game that is enjoyed can deliver far more practice
than a set of examples and she claims that the level of repetition would be
unreasonable in some games if they did not have some pleasurable outcomes. A
team of American researchers Bright, Harvey and Wheeler (1979) have carried
out many studies of the use of games to teach mathematics. Two of the studies
involved the use of games to reinforce basic multiplication and division facts
with single digit factors. 14 classes of 9, 10 and 11 year olds in 1976 and
10 classes of 10 and 11 year olds in 1977 played the games for 15 minutes daily
for a total of 7 days. Gains in test performances showed that the games treatment
was an effective way to retrain and reinforce children's skills with basic number
facts. A further study by Bright and Harvey (1982) involved supplementing regular
instruction on decimal fractions with the playing of a game. Some students in
the class played the game regularly in 20 minute sessions over a period of a
few weeks the remainder of the class only received regular instruction. A test
monitoring improvement showed that all the children improved over the few weeks
and progress for those children playing one of the games was significantly better,
with another of the games they concluded that there seemed to be no added effect
due to game playing. Ernest (1986) claims that the success of mathematics teaching
depends to a large extent on the active involvement of the learner. Playing
games demands involvement. Games cannot be played passively they have to be
actively involved, for this reason psychologists including Piaget, Bruner and
Dienes suggest games have a very important part to play in learning, particularly
in the learning of mathematics. Dienes (1963) even suggests that all mathematics
teaching should begin with games.
2. Ways of working
Paragraph 243 of the Cockcroft Report (1982) that stressed that children need
to discuss mathematics as well as learning it. There are many forms of discussion
built into the playing of games. The simplest is when a player explains to another
why a particular move is, or is not, legitimate. There are also occasions when
peer tuition emerges, notably in co-operative games. Hatch (1998b) suggests
that this can be encouraged in many games by using pairs of pupils working together
as a 'single' player. A lot of discussion then builds up as to the next move.
Kirkby (1992) says 'the value of discussion cannot be overstated. It is most
effective within small groups of two or three' (pages 6-7).
Children playing a mathematical game against each other co-operate playing
the game and if they play in teams they quickly learn that to play effectively
they must co-operate. Thus playing games provides an opportunity for children
to work co-operatively, a recommendation from the DES report (1985) Mathematics
from 5 to 16.
Games put pressure on players to work mentally. As Hatch (1998b) observes 'one
does not record anything while playing a game unless one has to. Players seem
readily to accept that when playing a game a calculator is not normally used;
indeed, it often slows the game unacceptably' (page 6). With the concern in
the UK about the mental skills of pupils and the pressure to improve them increasing
she claims that 'games involving numbers are a rich sort of the kind of practice
which is needed' (page 6).
Within the normal classroom situation there are few opportunities and little
incentive for pupils to check and justify their work. However within games since
cheating is something most children are conscious of there is a strong incentive
for players to check each other's mathematics, challenging moves which they
think are unjustified.
Some mathematical games provide the opportunity for pupils to make predictions.
This could be predicting the consequences of a particular move, deciding whether
to go or not; it may be better to miss a turn than to make a move which will
ultimately make your position worse. In Percentage Rummy (described on page
10) there may be several possible moves available, and several predictions may
be necessary to decide which is the best.
3. Pupil experience
Probably the most powerful reason for introducing games into the mathematics
classroom is the enthusiasm, excitement and total involvement and enjoyment
that many children experience when playing games. As Ernest (1986) notes, '
pupils become strongly motivated, they immerse themselves in the activity, and
over a period of time should enhance their attitude towards the subject' (page
2). Games are played in a context in which there is usually help available,
Hatch (1998b) found that groups are usually supportive of each other, solving
problems for people who are stuck and offering effective peer tuition. Kirkby
(1992) too notes the need for pupils to experience success, satisfaction, self-confidence,
enjoyment, excitement, enthusiasm, interest and active involvement. He believes
that there is 'no medium more powerful for providing these experiences than
the use of games' (page 5).
Disadvantages of using games
Of course there can be disadvantages to using games in the classroom. An understandable
worry about including games in mathematics is that this may introduce an added
element of competition in the classroom. Ainley (1988) recognises that teachers
who work hard to achieve a co-operative atmosphere in their classrooms may feel
that the introduction of games would be counter-productive. She points out that
games are often offered as a reward for those who have finished their 'work',
the hidden messages are clearly that real mathematics cannot be fun and that
games are not difficult 'work'. Hatch (1998b) also recognises a heightened noise
level, not as much written evidence as managers or parents might like and the
need for a lot of organisation of materials as possible disadvantages of using
games in the mathematics classroom.
CLASSROOM INVESTIGATION
I decided to use two games in the classroom to try to improve mental arithmetic skills. I felt this would be most productive if it focused on a particular topic, so my first task was to determine a suitable topic.
All the pupils in the class will be entered for the levels 3-5 examinations
in the SATS and therefore will attempt the lower tier mental arithmetic test.
As a starting point I gave them a previous test at this level (the sample 1997
paper, shown in Appendix 1). After I had marked them I recorded their results
in a grid (shown in Appendix 2). For each pupil I noted whether they had got
the question, right, wrong or not attempted it. I then looked at the questions
that had the highest number of incorrect or missing answers. As expected there
were a range of topics which the pupils had problems with. However what seemed
to be the most common thread was the relationship between fractions, decimals
and percentages and doing simple calculations with them, so this is the area
I have concentrated on.
To measure the effectiveness of the experiment I wrote a short diagnostic mental
arithmetic test covering only the target topics. I used this before I tried
the games and then again after we had played the games to see if there was a
marked improvement in performance. The test appears in appendix 3 and the initial
answers are analysed in appendix 4 using the same grid format as before with
the final test results appearing in appendix 5. Only results for pupils who
were present for both the initial and final diagnostic tests are recorded.
After the initial test the questions causing most problems seem to fall into two groups:
Game 1 - Find the missing number
This game is based on the game of the same name in Hatch (1998a) page 33. I
have however modified the contents of the cards to tie in with fractions, percentages
and decimals.
Using the set of cards below, three cards are dealt to each player who places
them on the table in front of them, the remaining cards are placed in a stock
pile. The dice is thrown by each player in turn ( moving clockwise) and if the
number on the dice is the correct missing number for any of the players three
cards then they win that card and replace it from the stock pile. The player
throwing the dice that turn is first to replace his card, then move clockwise.
The winner is the player who has won the most cards when the first of the players
runs out of cards.
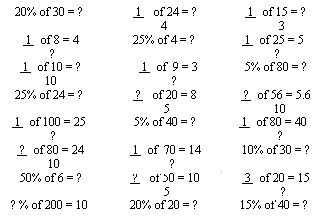
I tried playing this game with the class on two separate occasions. The first
time I set aside a whole lesson the second time a period of twenty minutes at
the end of a lesson.
The class has quite a few awkward characters in it and some time ago I drew
up a seating plan which moved pupils away from their friends. For this game
they were arranged in groups of 3 or 4, more or less where they would normally
sit, away from their own friends. The first few minutes of the lesson were very
difficult, the rules of the game were actually quite involved and many of the
class had difficulty working out what they actually had to do to play the game,
let alone how to cope with the mathematical content of it. I ended up moving
around the five groups going through the motions of playing the game with each
of them. The cards themselves seemed to fall into three categories, ones that
they could easily cope with such as:
1 of 24 = ? 50% of 6 = ? 10% of 30 = ?
4
ones that someone in the group could deal with and was prepared to help with,
such as:
![]()
and finally some cards which no one had much idea what to do with and they
resorted to asking me. Cards like these, all of which required a reverse process
which was either not straightforward or involved unfamiliar numbers:
![]()
This proved to be very time consuming for me and left me with little time to actually watch the class playing the game properly.
Most pupils worked out the value of their three cards and because for many of them this proved to be quite a difficult exercise at the beginning they wrote (unprompted by me) the missing numbers in the back of their books. This practice seemed to reduce as the game progressed. The other technique I noticed with a few students was for them to arrange their cards in order based on the numerical value of the missing numbers, they found this to be helpful when they played the game. I myself had used this when I had tried the game out.
By the time most groups were on to playing the second or third game they had
mastered the logistics of playing the game and many of them felt more confident
with the mathematical content of it. After about thirty five minutes some of
the naughty boys and girls in the groups were developing ways of cheating and
at this point we left the game and moved onto other work. A few days later I
played the game for a period of about twenty minutes at the end of a lesson.
The more motivated members of the class were keen to play and had remembered
the basic rules of the game, many of them had however forgotten how to cope
with some of the cards particularly the third category mentioned above, although
the game generated a good deal of discussion certainly in some of the groups.
Once again there were problems with some of the pupils in the class and
reluctantly I had to remove them from the game situation. For some of these
pupils the competitive instinct was too strong and winning no matter how had
proved to be too strong a motive.
After the two sessions on the game I was reluctant to play it again, there was not much enthusiasm to play it again and many had found the content had been too difficult to cope with in a game.
Game 2 - Percent Rummy
This is taken from Kirkby (1992) page 38, and is based on the well known card
game. The pack consists of the cards below and is made up of 12 groups, each
with 4 cards of equivalent value:
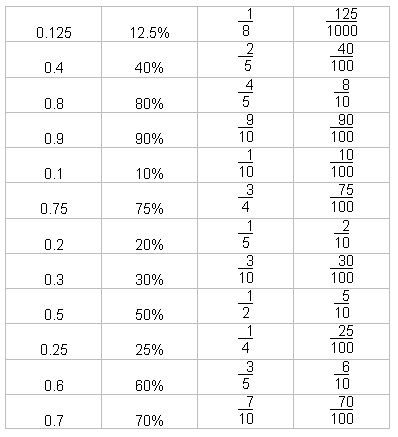
If there are two players then each is dealt ten cards, if there are three of
four players then each receives seven cards. The remainder of the pack is placed
face down in a stock pile.
The top card is turned up and discarded face up next to the stock pile. The
player to the left of the dealer takes the top card from either the stock pile
or the discard pile. He/she then attempts to lay down groups of three or more
cards of the same value. Finally he/she must discard one card onto the discard
pile. Once a player has put down a group, he/she may also add a card to groups
formed by other players. The first player to discard all his/her cards is the
winner.
From the beginning this game proved to be much more successful. Once again the logistics of playing the game needed careful explanation, several of the class were not familiar with the game and those that were tried to extend percent rummy to include runs which are allowed in the normal rummy game. This time I let the class sit in friendship groups and this too proved to be more successful, many of them felt like they were playing 'proper' card games to the extent that chewing of gum seemed to be widespread during the game.
For the purposes of this experiment the class played the game on two occasions.
As with the first game I allowed most of a fifty minute lesson the first time
for them to come to grips with it, and then a second session of twenty minutes.
The first time we played the game there was a great deal of discussion with
pupils asking each other whether cards were equivalent, the group of cards involving
one eighth caused the most problems but by the end of the two sessions most
of the class seemed to have remembered this group. The cards involving tenths
they were very happy with and many of the pupils seemed pleased with themselves
that they had grasped the connections. The only cards that still seemed to be
a problem to many of the pupils at the end of the second session were the groups
involving:
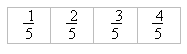
Linking these fractions with the remainder of their group requires a more sophisticated
understanding of equivalence than most of the other groups which only require
the link between tenths and hundredths.
Results of diagnostic test
Analysis of the diagnostic test after the use of the games reveals some interesting
findings. The average mark for the class went up from 56% to 68% and no pupil
got a worse mark on the final test than the first one. One of the most enthusiastic
participants in the games nearly doubled her score from 8 to 15 marks out of
20. The improvements are clearly related to improvements on particular questions.
Changing from decimals to fractions improved significantly as table 1 shows:
Question
number Decimal to change to a fraction Incorrect answers on first test Incorrect
answers on final test
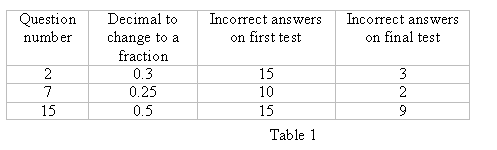
As well as the improvements in the answers to these questions there were clear
shifts to thinking in terms of tens and hundreds. Table 2 shows the change in
response to
question 7 changing 0.25 to a fraction.
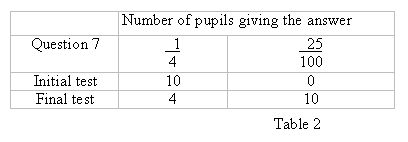
Surprisingly however 0.5 caused the class much more problems than any of the
other conversions, even though there has been a big improvement still more than
half of them are getting this wrong, table 3 on the next page shows the pattern
of errors.

Other conversions from fractions to decimals and percentages also showed big
improvements with fractions in the tens system being easier to cope with as
can be seen from this table.
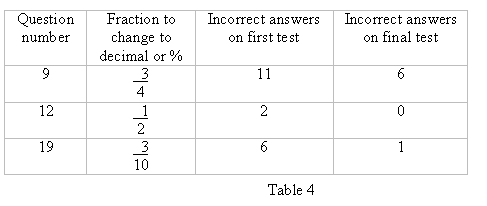
All these questions were addressed in the percent rummy game. The other questions showed very small improvements (mostly an extra 1 or 2 pupils getting them right).
CONCLUSION
The playing of these two games has given pupils the opportunity to practice
and reinforce the skills associated with some mental calculations involving
fractions, decimals and percentages. Pupils were very actively involved with
the Percent Rummy game, but many had great difficulties with Find the Missing
Number and I feel that after a while they 'switched off' .The diagnostic test
that was administered before and after the test shows big improvements on the
skills practised in Percent Rummy, namely the connections between common fractions
and their decimal and percentage equivalents. There is no noticeable improvement
on skills practised in Find the Missing Number game. This is in common with
the research by Bright and Wheeler (1982) who also had varying success with
their games.
The games provided pupils with different ways of working. Both involved pupils
working in groups and it was noticeable with this particular class how important
the make-up of the group was. Friendship groups seemed to be more successful,
I suspect because it tended to keep the more distruptive pupils together rather
than spreading them throughout all the groups. Pupils within friendship groups
also tended to work co-operatively discussing the game and the validity of various
answers.
Although I had not mentioned the use of calculators to the class they clearly
felt they were not appropriate and one or two pupils were told by the rest of
their groups to put them away, putting pressure on them to work mentally. In
the first game Find the missing number pupils certainly found a high proportion
of the calculations difficult to perform and many pupils noted answers down
to avoid repeating calculations unnecessarily. Within both games pupils checked
each other's work and when there was any doubt a pupil was called upon to justify
their answer, very occasionally I was called into provide the final word but
certainly in Percent Rummy each group resolved their own disagreements. Within
Percent Rummy there are many choices to be made about what to do next, most
of these are not obvious to the observer but cries of "I don't know which
to throw away" were quite common towards the end of the game and obviously
pupils need to make predictions and work through the consequences of each option
in their own mind.
As well as the advantages of playing the games there were disadvantages. Both the games I had chosen involved packs of cards, these were fairly time consuming to make especially as each group had different coloured cards. The different colours did help to keep each set of cards separate but there was always the need to make sure each pack was complete at the end of a session: it is amazing how many cards get dropped on the floor and how many pupils can't accurately count up to forty-eight! I was reluctant to leave the Find the missing number game when pupils were still not mastering it but I was very conscious of the need for pupils to the enjoy games and when a significant element of the class were struggling and clearly enjoyment wasn't the major reaction, I felt it was better to leave it. A great deal of effort had gone into producing a resource that had not been used very much, however there is always the chance to use them with a more able group.
The noise level was significantly higher during these games sessions, this was
not just increased discussions between pupils but also the fact that excitable
pupils also tend to shout rather than talk. I was particularly surprised at
the increased incidence of gum chewing during games and this was also evident
with a top set that I used Percent Rummy with, it was clear from the conversations
I had with them that they felt like they were playing cards with friends and
chewing gum was part of that experience. With this year nine class I did feel
that these games session were very hard work, there are several pupils with
behavioural difficulties and they responded differently to the games situation.
The most awkward boy in the class loved playing the games and was no trouble
at all, however there were a couple of other boys who were determined to win
whatever method was used and they together with a girl who was very good at
disrupting the games did cause problems. Generally they were containable for
a while and then had to be moved out of the games situation and on to other
work.
Overall I was pleased with my efforts on Percent Rummy, the children enjoyed the game and their mental arithmetic scores improved as a result of it, as an added bonus I have used this game with other classes. I never felt comfortable using Find the missing number with this class, it may however be successful with more able chuldren. Many of the class really enjoyed their time playing these games. As we had usually done this on a Friday they now have an expectation of playing games for part of the lesson on Friday and we have tried many other games that I had discovered in my research for this experiment. Clearly children can and do enjoy games in the mathematics classroom but initally it does require a great deal of preparation and testing to see which are appropriate. Having done that preparation they are a valuable resource that can be used repeatedly, sometimes with many classes.
REFERENCES
Ainley, J. (1988) Playing games and real mathematics, in Pimm, D (ed) (1988)
Mathematics, Teachers and Children London: Hodder and Stoughton
Bright, G. W., Harvey, J. G. and Wheeler, M.M. (1979) Using Games to Retrain
Skills with Basic Multiplication Facts Journal for Research in Mathematics Education
10(2)
Bright, G. W. and Harvey, J. G. (1982) Using Games to teach fraction concepts
and skills, in Silvey, L. and Smart, J. R. (eds) Mathematics for the Middle
Grades(5-9) Reston : NCTM 205-216
Ernest, P. (1986) Games: a rationale for their use in the teaching of mathematics in school Mathematics in School 15(1) 2 - 5
Cockcroft, W. H. (1982) Mathematics Counts, London: HMSO
Department of Education and Science (1985) Mathematics from 5 to 16, London:HMSO
Dienes, Z.P. (1963) An Experimental Study of Mathematics Learning, New York:
Hutchinson
Hart, K. (1981) Children's Understanding of Mathematics: 11-16, London: John
Murray
Hatch, G. (1998a) Replace your mental arithmetic test with a game, Mathematics in School, 27(1), 32- 34
Hatch, G. (1998b) A rationale for the use of games in the mathematics classroom, Topic Issue 19 (Spring 1998) NFER
Kirkby, D. (1992) Games in the teaching of mathematics, Cambridge:CUP
Kouba, V.L., Zawojewski, J.S. and Struchens, M.E. (1997) What Do Students Know
about Numbers and Operations? in Kenney, P. A. and Silver, E. A. (eds) Results
from the Sixth Mathematics Assessment of the National Assessment of Educational
Progress,
Reston:NCTM
Appendix 1 : Sample SATS mental arithmetic test from 1997

Appendix 2: Analysis of answers to sample SATS mental arithmetic test from 1997
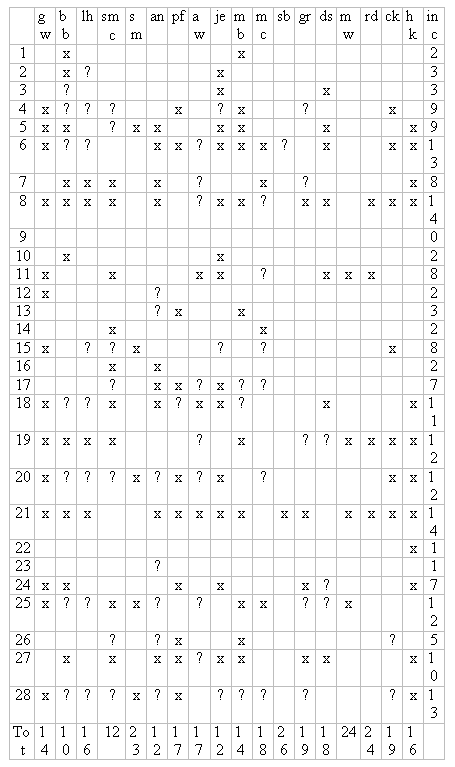
Each numbered line corresponds to that question number. Each column represents
a different pupil. Blank squares denote a correct answer, an x denotes an incorrect
answer and a ? shows the question was not attempted. The final column (inc)
shows how many pupils did not correctly answer that question.
Appendix 3: Diagnostic mental arithmetic test
1. What is 10% of 50?
2. Write 0.3 as a fraction.
3. What is 57 x 10 ?
4. Half of a number is 6, what is the number?
5. What is 1/3 of 75?
6. What is 20% of 70?
7. Write 0.25 as a fraction.
8. What is 62 x 100 ?
9. Write 3/4 as a decimal.
10. What is 1/8 of 56?
11. One quarter of a number is 30, what is the number?
12. What is 1/2 as a percentage?
13. What is 4.3 x 10 ?
14. What is 15% of 80?
15. Write 0.5 as a fraction.
16. 1/8 of a number is 5, what is the number?
17. What is 3.4 x 100 ?
18. 25% of a number is 10, what is the number?
19. Write down 3/10 as a percentage.
20. What is 2.7 x 1000 ?
Appendix 4: Analysis of diagnostic mental arithmetic test before playing the
games.

Each numbered line corresponds to that question number. Each column represents a different pupil. Blank squares denote a correct answer, an x denotes an incorrect answer and a ? shows the question was not attempted. The final column (incorrect) shows how many pupils did not correctly answer that question.
Appendix 5: Analysis of diagnostic mental arithmetic test after playing the
games.
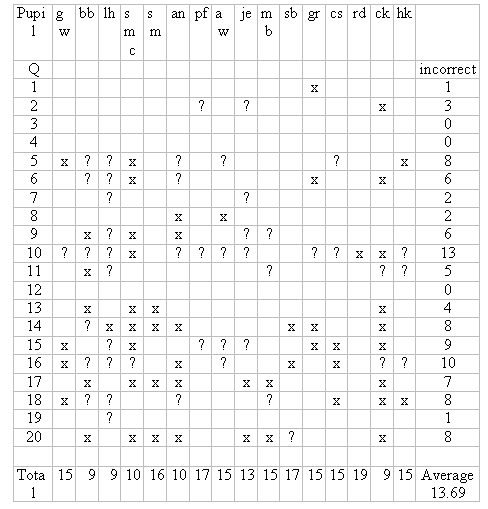
Each numbered line corresponds to that question number. Each column represents a different pupil. Blank squares denote a correct answer, an x denotes an incorrect answer and a ? shows the question was not attempted. The final column (incorrect) shows how many pupils did not correctly answer that question.