
Sharon Friesen, Galileo Educational Network
Patricia Clifford, Galileo Educational Network
David W. Jardine, University of Calgary
Introduction
The light dove, cleaving the air in her free flight, and feeling its resistance, might imagine that its flight would be still easier in empty space.
Immanuel
Kant (1767/1963). From the Introduction to his
Critique of Pure Reason
.
This passage was originally written as a way to begin a critique of those forms of philosophical idealism which speculatively shun the resistance and troubles and lessons of the world, lessons which might, in their resistance to the flights of reason, help shape and strengthen and measure our philosophizing.
This invocation of an Earthly measure is not meant as an embarrassment to philosophizing per se, but as a reminder that the sense of reasonableness that our lives require we think especially of the lives of teachers and students in school classrooms-- require of reason that it maintain a sense of proportion, of properness, of having to worn the midst of the frail conditions of human existence.
We are especially taken with this image of the dove and its flight in two nearly-contradictory ways. First of all, we have encountered countless situations in which constructivist, post-modernist or chaos theory work becomes so speculative that, as practising teachers faced with the exigencies of everyday life, we become unable to recognize our own troubles in their philosophical flights. We have argued, with varying success, for the ways in which our thinking must find its thoughtfulness through the worldly work, in the face of the testy case that will slow thought down and test its resolve, its strength, its patience and its worth.
Secondly, however, we also find the opposite trouble appearing:
when we delve into attempting to describe and explore the stubborn particulars
of classroom life and classroom conversation, no amount of detail seems to be
adequate to its living thoughtfulness and it is all too easy to get lost in
the thickets of particularity.
In fact, thickening the dove’s air is as troublesome
as the desire for no resistance at all. So, we search for that tenuous balance,
one deep in the heart of our very mortality to say what we have seen, to think
and speculate and soar, and to live well with the obligations that education
puts us under, with this student, here, now, Jenny and her shapes.
It Begins with Jenny’s Shapes
"It's a poor sort of memory that only works backwards," the Queen remarked
Lewis Carroll, Through the Looking Glass
The story begins with Jenny at work.
She sits at the end of one of the tables in our classroom. Her long dark hair falls onto her paper as she methodically calculates then meticulously measures each new line. Placing her ruler across the two points that she has calculated and measured, she ever so carefully draws the first light pencil line. Then checking to ensure the accuracy of the line, Jenny draws the second, now darker line over the first line. She removes the ruler from the paper and critically analyzes her work. "Good, it's good," she seems to say. And then she repeats the process, recursively adding the next and then the next line to the geometrical drawing.
Sometimes a smile of intense satisfaction crosses her face.
Sometimes fellow students come by to inquire about her work. "Wow
Jenny, that is so beautiful," they say as they admire the emerging form.
Jenny smiles and then goes back to calculating, measuring and drawing.
Each line is precise. Each calculation is exact.

Pat and I also watch Jenny as she works on this construction. Images of Basle's (1583) Margarita philosophica come to mind in which geometry is depicted as a contemplative practice, "personified by an elegant and refined woman, for geometry functions as an intuitive, synthesizing, creative, yet exact activity of mind associated with the feminine principle" (Lawlor, 1982, 7).
Deeply immersed in the traditions of geometrical ways of knowing and doing that have "arisen within our human space through human activity" (Husserl, 1970, 355), Jenny has come upon "an inner logic so profound that every critical piece of it [contains] the information necessary to reconstruct the whole" (Palmer, 1998, 123).
It also begins with the Pythagorean theorem
Pat and
I learned the stories of the mystical Pythagoras and his disciples when we first
set out on this journey together in our irregularly shaped classroom with fifty-some
Grade 1/2 children. Now here we were, once again telling the secrets of
these early mathematicians and their quest to unite numbers and shapes to fifty-some
Grade 8 children. These students were just as enchanted by the stories
of these ancient radicals as the younger children had been. "Good
mathematics ultimately comes from and returns to good stories and the questions
that bug you" (Casey and Fellows, 1993, 1) stories that have the power
to open an engaging mathematical). In this space, right angle triangles
are so much more than finding the length of the hypotenuse using the handy formula
a theorem that stills bears the Pythagorean name.
Invoking a 3-4-5 triangle and unfolding its beauty and simplicity necessitates the story of a man, an outcaste. How else can we let the students know that this simple formula carries with it the weight of history? It stands the test of time. It still stands as a pillar in trigonometry. This act of measurement is a fundamental one that reaches back to Ancient Egypt. Using a rope knotted into 12 sections stretched out to form a 3-4-5 triangle, rope-stretchers reclaimed and reestablished the boundaries of land and set order to the watery chaos created by the annual flooding of the Nile.
Reaching back in time, the Pythagorean theorem is one of the earliest theorems to known ancient civilizations. There is evidence that the Babylonians knew about this proportional relationship some 1000 years before Pythagoras (Siefe, 2000, 29). Plimpton 322 , a Babylonian mathematical tablet which dates back to 1900 B.C., contains a table of Pythagorean triples -4-5, 5-12-13, 7-24-25... The Chou-pei , an ancient Chinese text, also provides evidence that the Chinese knew about the Pythagorean theorem many years before Pythagoras discovered and proved it (Joseph, 1991).
And it begins with an exploration
"Draw a right angle triangle. Any sized right angle triangle. Using only triangles that are similar to and/or congruent with your original, I want you to explore the properties of right angle triangles."
My instructions were very simple. The story had already charmed the students and generously bounded the territory of the exploration. I provided these few directions to start our mathematical journey, and then we all began.
What a strange place to be teaching like
this
. We were in the heart of East Calgary. These students scored in the lowest quartile in the entire province. Our colleagues told us that what these students needed were "the basics."
"Make them memorize their basic facts."
"Give them real life problems. You know problems like calculating how much change they need to give someone. Or how much money they will need to earn to buy groceries. Or how much material they will need to purchase in order to make the items that their customers desire."
We seldom entered into the exhaustive debates that these well-intended comments opened. "What if this is not the way that mathematics exists , as object either produced or consumed, either individually or collectively" (Jardine, Friesen, and Clifford, 2000, 3)? Having endured seven years of consuming and producing mathematics, these students were very clear about their regard for math. "We HATE math." "It's boring." "We are never going to need it." "We'll just get a calculator." These students who were bored and turned off almost from their earliest days in school, who could not (or would not) read, who knew far too little mathematics, who would stop taking science as soon as they could get away with it, who dropped out of school at worrisome rates. It is with these students that we now taught like this .
Jenny's quest to understand these dynamic spirals continued.
When we saw her drawing of four tessellated, symmetrical patterns, we
were awed. To produce such a stunning beautiful piece of work by hand
certainly required contemplation and exactitude beyond what we could have ever
hoped for. And for us, this would have been enough, but not for Jenny.
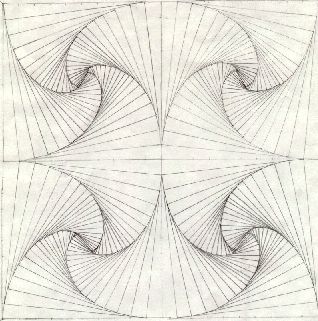
She continued to ask questions of this beautiful form and its symmetry, and each new question led us all deeper into this exploration. Spiral doodles started to appear all over the classroom on notebooks, scraps of paper, borders on assignments. Some students started to create a variety of spirals using the Logo program we had in the classroom. They learned the power of variables. Creating the following set of commands:
TO POLYGON :SIDE :ANGLE :AMT
IF :SIDE>300 [STOP]
FD :SIDE
RT :ANGLE
POLYGON (:SIDE + :AMT) :ANGLE :AMT
END
produced this spiral:
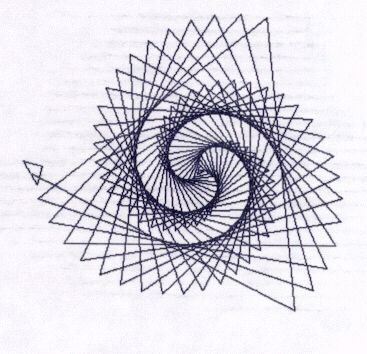

 Chad, age 1
Chad, age 1
We were experiencing what it meant to create new mathematics. We were beginning to understand how creating new mathematics begins with asking questions. Sometimes a question that is easy to ask is impossible to answer. Sometimes a question that sounds difficult turns out to be something you already know, just dressed up to look different. Sometimes the question leads, not to an answer, but to another question. And for these questions, the answers are not in the back of the book. It's the posing of questions that kept calling us on to new possibilities, wondering what might be around the next corner, helping us to understand that mathematics is not finished, it's work in progress, it's a " living, breathing, contested, human discipline that has been handed to us" (Jardine, Friesen and Clifford, 2000, 4).
Working in 3D
Working on the two dimensional plane was intriguing and engaging, but what about 3D? Our questions were quite playful as we started, "I wonder what would happen if " " I wonder if the symmetries that we had found on the 2D plane would hold as we tiled them onto the surfaces of a solid."
We decided to begin by tiling the surfaces of regular solids known as Platonic solids: tetrahedron, icosahedron, dodecahedron, octahedron, and cube with the various symmetrical designs that we had constructed. What better place to try out our emerging understandings than on such perfectly symmetrical solids. Each of our geometric models began as a flat design. We not only had to determine the shapes of the sides we needed to construct in order to create the transition from the two dimensional net to the three dimensional solid, we also needed to figure out how to place our designs on the two dimensional plane so they it would be perfectly symmetrical in three dimensions. The two dimensional pattern gives few clues as to what you will see and feel when it takes shape in three dimensions.
The flat designs represent the possibility of infinite repetition but only a fragment of this infinity can be captured on a sheet of paper. On the surface of a three-dimensional object, infinite repetition of design can be realized with only a finite number of figures the pattern on a solid has neither beginning nor end" (Schattschneider and Walker, 1982, 16).
Creating the nets for each of the solids was fairly challenging,
but determining how to draw the designs onto the surfaces so that they would
come together to produce the illusion of infinity was exigent. "Contrary
to the impression given by most textbooks, the discovery of new forms and new
ideas is rarely the product of the predictable evolution" (Schattschneider
and Walker, 1982, 8). After many attempts the student's solids began
to take shape. They were pleased.

Chad and Ricky - age 13
But it was Jenny who really pushed our thinking. It
was Jenny and her love for the logarithmic spiral that pushed us to the frontiers
of mathematics itself.
Starting with the cube, Jenny drew the curves on each of
the six faces. Upon assembling the cube she discovered that the designs
did not flow. The symmetry was broken. How could symmetry be lost
on this perfectly symmetrical solid?

Believing that she had made an error, she drew another
cube. This time she transformed the spirals by reflecting them. However,
upon putting the net together, she discovered that the problem was not solved.
The pattern of the curve had broken the symmetry of the perfectly symmetrical
cube Greek symbol of earth. The act of reflection had not solved the problem.
How could that be? What would work? "I want to find out why the symmetry
breaks," Jenny wrote. "I am going to see if I can make the symmetry
work on any of the other solids. If I can, then maybe I will know why
it doesn't work on the cube."
Creating the curves on four equilateral triangles, Jenny
started on her consuming quest to understand more about symmetry. She
created the tetrahedron the symbol of fire.

Intrigued by her new discovery and undaunted by her disappointment, Jenny took on the challenge of the octahedron air.
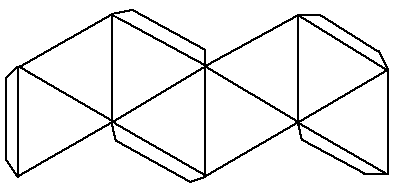
Once again, working on the two dimensional equilateral
triangles, Jenny meticulously measured and drew what we all now called "Jenny's
curves."
Magic "It was like magical," Jenny later wrote.
As Jenny folded the edges of these eight equilateral triangles together
form and design came together, symmetry held and infinity emerged from the finite.

What was it about the octahedron that was different from the tetrahedron or the cube? Everyone in the classroom was now involved in Jenny's problem including Pat and me. Was there a solution? "If there is, I don't know it," Jenny wrote. "There might be an easy way to figure this out, but I don't know it. I will draw an icosahedron. It's faces are also triangles."
For Jenny, as for all of us, we thought that the solution
might be in the shape of the faces themselves. The tetrahedron did not
work. But it was small it only had four faces. Perhaps there was
something in the number of faces. The octahedron had eight faces. Why
should the symmetry hold with eight fven numbers. But so was six
for that matter the number of faces on the cube. The solutifour. Maybe
there was something in that. Maybe there was something in the odd and
the even. Like the ancient Pythagoras, we went looking for a connection
between shapes and numbers.
Jenny continued drawing. Her next shape was the beautiful,
perfectly symmetrical solid icosahedron, representing the Greek symbol for water.
Upon each of its twenty identical equilateral triangle surfaces, Jenny
drew the logarithmic spiral.

As she brought each of the five vertices of the solid together, she discovered, as did we all that symmetry was lost. But why? There had to be a solution.
It would be easy to conclude that we were just involved in solving the problem posed by Jenny's shapes. But that is not really what was happening at least not all that was happening. Mathematics is not just a problem solving activity. We were involved in something far more fundamental far more "basic" to mathematics. We were caught up in a generative act "the central activity being making new mathematics" (Wilensky, 1996). It was consuming for all of us. We noticed the students puzzling with the various shapes, trying to put them together in different ways, trying the dodecahedron, looking again at previously failed symmetries whenever they found breaks in their normal day-to-day studies. Pat and I puzzled along with them.
While driving home from school one day along the busy, accident-riddled
Deerfoot freeway I had a flash of insight. I suddenly knew a direction
to take that might hold the key to Jenny's shapes. I pulled over
to the side of the road and frantically dug through my books for a piece of
paper and a pen or a pencil. That's it. Flatten the shape.
Step on it. Make a graph. Not the normal school type graph
a statistical graph, but a network, that type of graph.
We had been playing with networks earlier in the year. I
had read the students the story Superperson Saves
the Monster (Casey and Fellows, 1993, 51). It
is a zany story about three characters: Gertrude the goose, Monster and Superperson.
Now suddenly on this freeway, driving home from school this story seemed
to somehow to hold the key to Jenny's shapes. "Sometimes ideas
are often born unexpectedly from complexity, contradiction, and, more than anything
else, perspective" (Negroponte, 1996).
"Look at the vertices," Jenny's shapes seemed to call. As I flattened each of the shapes, about their vertex points, I noticed that the vertices and edges came together in a pattern of odds and evens. The tetrahedron three, the cube three, the octahedron four, the icosahedron five. There it was. I could hardly wait to get back to school the next day. I needed to let the class know that the Superperson story might hold the key. Upon revisiting the story, the students saw it too. "I don't think I need to make a decahedron," wrote Jenny. "It has an odd number of edges at the vertices."
I still had some reservations. How could we be sure
that we were right? I packed up all of Jenny's shapes and took them
to a mathematician at the university. I told him the story of Jenny's
shapes and showed him how we had come to a solution. "Does this make
sense to you, Claude?" I asked.
"Let's see." Claude drew a number of
sketches on the chalkboard in his office. "Yes, I believe you and
your class are on to something," he said. "The direction
you have chosen seems to be a good one."
"But are we right?" I wanted to know.
"I don't know," he said. "But it
looks like you are in an exciting and productive place. This is all new
mathematics. There are people here who know more than I do about this
area. You are creating mathematics."
We began our exploration with Euclidean geometry but now
we found ourselves in a very different space a geometrical space that had more
questions than answers. It seemed as though we had left the deeply familiar
Euclidean geometry behind and were pushing at the very frontiers of mathematics
itself non-Euclidean geometries. It was an exploration that drew us in.
"It [pulled] us into its
question, its repose,
its regard. Therefore,
first is the question posed, not by us
but to us " (Jardine,
Friesen and Clifford, 2000, 6)? We were consumed by the questions that
kept presenting themselves, that kept calling to us from Jenny's shapes.
Where was Pythagoras? Did we leave him behind? Or are we in a place that required Pythagoras? Were we standing in the "long and twisted entrails of all the interdependencies that gave rise to [what was] being manifest, just here, just now" (Jardine, Friesen and Clifford, 2000, 7)? Did Pythagoras, in his explorations and eccentricity know was he preparing a place which could give "birth" to this new mathematics? A place that could support Jenny's quest. A place large enough for all her classmates and her teachers. A place that required us all and all of us. "Mathematics
is
, in some sensible sense, all the actual human, bodily work which is required if it is to remain hale and healthy, if it is to continue as a living practice which we desire to pass on, in some form, to our children" (Jardine, Friesen and Clifford, 2000, 12).
REFERENCES
Berry, W. (1983). Standing by words . San Francisco: North Point Press.
Casey, N. & Fellows, M. (1993). This is megamathematics! Los Alamos, New Mexico: Los Alamos National Laboratory. Also available from Internet: http://www.c3.lanl.gov/megamath/menu.html.
Dyson, F. (1996). "The scientist as rebel." American Mathematics Monthly , 103, 9: 800805.
Friesen, S. & Stone, M.G.. (1996). "Great Explorations." Applying Research to the Classroom 14,2: 611. Available online: http://www.galileo.org/math/sumtalk/problem.html.
Holding, J. (1991). The investigations book . Cambridge: Cambridge University Press.
Husserl, E. (1970). The crisis of European sciences and transcendental phenomenology . Evanston: Northwestern University Press.
Jardine, D. W., Friesen, S. & Clifford, P. (2002). "Behind each jewel are 3000 sweating horses: meditations on the ontology of memory in mathematics education." In HaebeLudt, E., and Hurren, W. (eds.) Curriculum Intertext: Place/Language/Pedagogy. New York: Peter Lang Publishing.
Joseph, G.G. (1991). The crest of the peacock: NonEuropean roots of mathematics. New York: Penguin.
Kant, I. (1767/1963). Critique of Pure Reason . London: MacMillan Press.
Lawlor, R. (1982). Sacred Geometry . New York: Crossroad.
Negroponte, Nicholas. 1996. "Where do new ideas come from?" Wired .
Available from Internet: http://www.wired.com/wired/archive//4.01/negroponte_pr.html
Palmer, P. (1998). The courage to teach: exploring the inner landscape of a teacher's life . San Francisco: JosseyBass Inc.
Pappas, T. (1989). The joy of mathematics . San Carlos, California: Wide World Publishing/Tetra.
Schattschneider, D. & Walker, W. (1982). M.C. Escher Kaleidocycle . Norfolk, England: Tarquin Publications.
Siefe, C. (2000). Zero: the biography of a dangerous idea . New York: Viking.
Wilensky, U.J. (1996). "Making sense of probability through paradox and programming: a case study in a connected mathematics framework." Available from Internet: http://ccl.northwestern.edu/cm/papers/paradox/lppp/