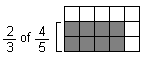
BELIEFS ABOUT WHAT EXPLAINING WHY MEANS FOR A STUDENT IN A MATHEMATICS CLASSROOM: A CASE STUDY
María del Valle Mina
Córdoba, Argentina, <sensei(at)infovia.com.ar>
@ is replaced by (at) to stop the automatic garnering of email addresses by Spam factories - Editor
INTRODUCTION
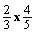 . The student responds
. The student responds 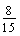 correctly and then, he/she is asked to explain why
correctly and then, he/she is asked to explain why
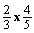 equals
equals
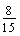 . A
straightforward explanation of the algorithmic rule
. A
straightforward explanation of the algorithmic rule 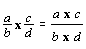 is often obtained, without no reference to why this procedure
really works. Nevertheless, it is expected that the student should relate
this rule to the learnt visual representation (see figure 1) which usually provides
a simple explanation for younger children.
is often obtained, without no reference to why this procedure
really works. Nevertheless, it is expected that the student should relate
this rule to the learnt visual representation (see figure 1) which usually provides
a simple explanation for younger children.

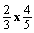 Addressing this situation can be viewed as a problem of cognitive demands (i.e. can students make or evaluate logical arguments?) on children. However, another
why-situation,
in a different context, casts some doubt on this interpretation.
For example, when a student complains to the teacher about an obtained score in a test, he/she expects that the teacher will give thoughtful arguments that underpin the assessment criteria.
In this case, the student will not accept just a marking procedure’s explanation from the teacher.
Addressing this situation can be viewed as a problem of cognitive demands (i.e. can students make or evaluate logical arguments?) on children. However, another
why-situation,
in a different context, casts some doubt on this interpretation.
For example, when a student complains to the teacher about an obtained score in a test, he/she expects that the teacher will give thoughtful arguments that underpin the assessment criteria.
In this case, the student will not accept just a marking procedure’s explanation from the teacher.
REVIEW OF LITERATURE
According to Schoenfeld, students’ beliefs shape their behavior in wn be conjectured here that if a student holds a belief that mathematics means just applying unreasonable given rules, he/she is likely to perceive a
why
question as if it were a
how
one (see Wood’s categories a and their very nature.
Beliefs about mathematics
Beliefs are defined as personal judgments about mathematics formulated from experiences in school (Raymond 1997, p. 552). These judgments can include what McLeod (1992) calls the objects of the beliefs: beliefs about the nature of mathematics, the learning of mathematics and the teaching of mathematics. In her perception, Raymond (1997) also points out the importance of past experiences in school mathematics in shaping personal beliefs of both teachers and students. Other perceptions also point to the influence of beliefs on how students conceptualize and do mathematics (Schoenfeld 1992). Drawing on these conceptual aspects, I consider mathematics beliefs as personal judgments about mathematics and doing mathematics formulated from experiences that shape the ways by which a student engages in any mathematical activity. I think that this perception encompasses relevant features about students’ beliefs and, at the same time, fulfills the present research requirements.
How beliefs develop and impact on behaviour
Two complementary perspectives are considered to conceptualize how beliefs develop and influence behaviour in mathematics classroom: the cognitive accounts of McLeod’s analysis of Mandler’s theory (McLeod 1992) and social constructivism (Ernest 1998).
McLeod considers beliefs, attitudes, and emotions as representing a wide range of affective responses to mathematics. In this range, beliefs appear as the more stable, more cognitively demanding, and less likely to result in affective involvement responses. Within a cognitive approach, McLeod highlights Mandler’s general theory of development in the affective domain and gives a brief summary of it:
Mandler’s view is that most affective factors arise out of the emotional responses to the interruption of plans or planned actions. In Mandler’s terms, plans arise from the activation of a schema. The schema produces an action sequence, and if the anticipated sequence of actio followed by a physiological response. This physiological arousal is typically felt as an increase in heartbeat or in muscle tension. al’s s phe. The cognitive evaluation of the interruption provides the meaning to the arousal. (McLeod 1992, p. 578)
In his analysis of the meaning of the interruptions, McLeod also provides some aspects which are relevant for the present study. One of them relates to the cognitive interpretation of these interruptions and the role of beliefs in it:
First, the meaning comes out of the cognitive interpretation of the arousal. This meaning will be dependent on what individual knows or assumes to be true. In other words, the individual’s knowledge and beliefs play a significant role in the interpretation of the interruption. The role of the culture that shapes these beliefs would seem to be particularly important. (McLe578)
For example, if a student holds a belief that mathematics means applying unreasonable rules, when confronted with a why-situation, he/she is likely to face an unpleasant experience and evaluate it as what mathematics has to do with this. This kind of facts in which beliefs influence behaviour in mathematics classroom, especially in problem solving context, has been widely reported in the literature (Schoenfeld 1987, 1992). Another part of Mandler’s theory considers how an emotion develops into the most stable of the affective responses, i.e. beliefs:
Third, repeated interruptions in the same context normally result in emotions that become less intense. The individual will reduce the demand on cognitive processing by responding more and more automatically, and with less and less intensity. The responses in this situation become more stable and predictable (McLeod 1992, p. 578)
Following the example above, how did the student come to believe that mathematics means applying unreasonable rules? Here, the repeated interruptions in the same context were probably characterized by working a lot of exercises by which mastering rules laid down by the teacher were needed. Consequently, beliefs about how to do mathematics and what it means to know in school are acquired through years of watching, listening and practicing (Lampert, quoted in Schoenfeld 1992, p.359).
Although the theoretical perspective stated above provides useful explanation about how beliefs develop and impact on behaviour from a cognitive point of view, I consider that a complementary approach is needed in order to elucidate another kind of classroom events: even though students are involved in discursive activities and challenged to explain their thought to others as a regular activity in classroom, they may still give how-answers to a why-questions.
From the teacher perspective, the context is viewed as argumentative (Wood 1999) but students perceive it as compelling procedural instructions.
The tenets of social constructivism (Ernest 1994a, 1998) enlighten this issue. This perspective considers a mathematical classroom as a complex, organized, and evolving social form of life (Ernest 1998, p. 231) in which students, not only learn mathematical content, but also learn to participate in a mathematical culture. That is to say, by identifying patterns of participation in a particular social context, students infer norms of
how
and
when
to interact with others and develop beliefs about these norms (Yackel and Cobb 1996). These authors distinguish between sociomathematical norms that regulate specific aspects of students’ mathematical discussions, and general social norms that control broad aspects of those interactions. To illustrate this point, I apply these ideas to the classroom event described above as In every mathematics classroom, it is expected that students explain their solutions and thinking to others (a general social norm), but which explanation is mathematically acceptable is a matical norm. Therefore, if a student infers from every class discussions that the teacher likes neat explanations of procedures, he/she is likely to give a
how
-answer when asked
why
, even though the rationale behind such procedure is known.
In short, beliefs play an important role in shaping students’ behaviour in mathematical classroom. A
how
-answer can be the result of a cognitive process influenced by held judgments about what explaining means in mathematics. At the same time, what becomes an accepted
why
-answer is also constrained by beliefs inferred from participating in a social context regulated by norms continually regenerated and modified by the students and the teacher through their ongoing interactions. (Yackel and Cobb 1996, p. 474) However, what makes one mathematics classroom different from another one leads to further considerations described in the following subsection.
The nature of beliefs about mathematics
Researchers have drawn attention to teachers as representatives of the mathematical community (Dossey 1992). Consequently, teachers play an important role in the determination of particular features of every classroom culture. In doing so, their held beliefs about mathematics, its teaching and learning, are determinant factors in the establishment of what constitutes a sociomathematical norm, as defined above (Cooney et al. 1998, Ernest 1988, Thompson 1992). It is argued that a philosophical perspective is needed to clarify the very nature of beliefs (Thompson 1992). Here, researchers confirm that any philosophy of mathematics has many categorical consequences when embodied in both teachers and students beliefs about mathematics (Ernest 1994b, 1996; Thompson 1992). Some features of the conceptions about mathematics, public images about mathematics (Sam 2002) and their influence in school mathematics are discussed below.
Ernest (1996) considers two perspectives, absolutist and fallibilist, in the philosophy of mathematics. According to Ernest, absolutist philosophies
[] view mathematics as an objective, absolute, certain and incorrigible body of knowledge, which rests on the firm foundations of deductive logic.
The outcome is therefore a philosophically sanctioned image of mathematics as rigid, fixed, logical, absolute, inhuman, cold, objective, pure, abstract, remote and ultra-rational. Is it a coincidence that this image coincides with the widespread public image of mathematics as difficult, cold, abstract, theoretical, ultra-rational, but important and largely masculine? Mathematics also has the image of being remote and inaccessible to all but a few super-intelligent beings with ‘mathematical minds’.
An absolutist view may be communicated in school by giving students mainly unrelated routine mathematical tasks which involve the application of learnt procedures, and by stressing that every task has a unique, fixed and objectively right answer, coupled with disapproval and criticism of any failure to achieve this answer. (Ernest 1996)
From the perspective of fallibilist philosophies,
[Instead] mathematics is associated with sets of social practices, each with its history, persons, institutions and social locations, symbolic forms, purposes and power relations.
Coinciding at least in part with the fallibilist philosophy of mathematics is the vital image of mathematics communicated in many progressive school and colleges. Mathematics is experienced as warm, human, personal, intuitive, active, collaborative, creative, investigational, cultural, historical, living, related to human relations, enjoyable, full of joy, wonder, and beauty. (Ernest 1996)
With the theoretical framework provided by these perspectives in mind, I conjecture that the way students perceive a why-situation is influenced by held beliefs about mathematics which compel them to answer as if the situation were a
how
one. Summing up, the point of interest for the present study is that every philosophy of mathematics has an associated conception of school mathematics and doing mathematics. Therefore, beliefs about what explaining
why
means in mathematics may be embodied in any of these particular conceptions. Exploring these beliefs and relating them to particular beliefs about mathematics were the purposes of this study.
THE INVESTIGATION
I conducted a case study (McKernan 1999) of one student in order to organize, and report on information about the actions, perceptions, and beliefs of an individual or group under specific conditions or circumstances (Romberg 1992, p. 57). For the present study, specific conditions or circumstances means why-situations in mathematics classroom. This method, particularly suitable to study beliefs, also offered some insight into how past experiences affect behaviour in learning mathematics, based on the reasonable assumption that not all such behaviour results from present interventions by the teacher.
Participants
I conducted the study in a secondary school with a low-socio-economic population in Córdoba, Argentina (an Spanish speaking country). Because I was interesting in studying beliefs as a result of past experiences, I selected the student from a class of 12-13 years old students since at this age, children have just passed from primary school to secondary school. Primary school mathematics in Córdoba is characterized by a procedural approach, whereas secondary schools are compelled to offer a more conceptual curriculum. Thus, it was more likely that students in their first year of secondary school would be puzzled and challenged by a teacher who asks them why do you think this? The subject (a 12-year-old girl) was selected after analysis of classroom observations. The student kindly agreed to be interviewed.
Procedure
Literature on research on beliefs in mathematics education suggests that a combination of techniques has a better chance to make a contribution to research about beliefs (McLeod 1992). Therefore, for the present study, data were gathered by classroom observation field notes, the particular student’s observation notes, and the particular student’s semi-structured interview transcripts.
Four scattered class period of 40-minutes was observed in order to select a prospective student and ascertain her behaviour in a whole-class setting. Ernest (1998)’s theorization
of
the social context of the school mathematics and its components provided a useful conceptual framework to develop every class observation, which included: the aims and purposes of the activity, the persons involved and their interpersonal relationships, the discourse and its social regulations, and the material resources. The student was selected after the first 40-minutes observation, according to the content of the student’s judgments, i. e., explanations regulated by a how aim rather than a way one, and the student’s disposition to spontaneously express his/her own ideas during whole-class interactions. The selormance in mathematics.
In order to gain an understanding of the particular student’s beliefs about what explaining
why
means in mathematics and about mathematics itself, a 20 minutes semi-structured interview was conducted along a previously elaborated questionnaire (see Appendix 1 for the translation from Spanish). Elaborating questionnaires used by Franke and Carey (1997) and suggested by Spangler (1992), I formulated two sets of open-ended questions. The first set of questions had the aim to ascertain how the student would perceive the sociomathematical norm that regulates explaining in why-situations by addressing the distinction between a how-question and a why-question, what kind of answers deserve teacher acceptance, and what a why-question means in a context apart from mathematics. The second set of questions intended to help me determine the student’s beliefs about school mathematics by addressing the stereotypes of mathematically talented people, resolving conflict when students’ answers were different, student’s acceptance of alternative waysons supported the students’ ability to articulate their thoughts and perceptions (Franke and Carey 1997, p. 12). The interview was transcribed verbatim and subsequently trnslated into English.
Results
Data gathered by classroom observation field notes, the particular student’s observation notes, and the particular student’s semi-structured interview transcripts are organized in terms of the context description, the description of the student’s behaviour in this context and her answers to both sets of questions. Every description is followed by its respective discussion.
1. The context
Every 40-minutes observed class was created to review learnt topics about data gathering, statistical graphs, and probability by checking students’ homework. Activity sheets and calculators were on hand to the students. Many mathematical symbols (fractions, percentages, and decimals), modespoken mathematics were used. The main mode of interaction between the teacher and her students was as follows: the teacher poses a question to thent to explain his/her solution; if the student’s answer is right, the teachers agrees, otherwistudent about why the theoretical probability of an event was 11/20, the teacher asked:
Teacher: Which is the numerator?
Student: 11.
Teacher: Ok. Which is the denominator?
Student: 20.
Teacher: Ok. The right answer is 11/20. Lets go to the next exercise ...
Examination of this kind of recurrent classroom interaction shows an inadequate context for helping students to distinguish between explanations that describe procedures and those that describe actions on experientially real mathematics objects (Yackel and Cobb 1996, p. 467). According to these authors, opportunities for learning an acceptable mathematics justification arise when children attempt to make sense of explanations given by others, to compare others’ solutions to their own, and to make judgments about similarities antween appropriate answers to
why
or
how
questions. Moreover, description of performed procedures are socially accepted explanation in why-situations in the observed classroom.
2. The student’s behaviour
Andrea (a pseudonym is used instead of students’ own name) was selected using the criteria stated above. Even though Andrea’s explanations were regulated by a how aim, they were concise, accurate and well-organized. She also stood out because of her willingness to respond to every teacher’s question. By means of her neat answers and pattern of participation in whole-class discussions, Andrea’s behaviour revealed her acquaintance with the sociomathematical norms supported in the observed classrooiew, Andrea pointed out making good explanations for the others as a feature of a good mathematics student (see Appendix 2, Transcript 1). Andrea’s perception of which answers are accepted by the teacher in why-situations also showed emphasis on the formal aspects of an explanation (step-by-streasons behind a why question were given here.
From these findings, I might conclude that Andrea shows a coherent behaviour with regard to the expectations of others. It is claimed that children are involved in learning what others expect of them in terms of participation as well as learning the content of lessons (Wood 1999, p. 174). Therefore, holding a view that explaining
why
means giving detailed procedural description as teacher likes, Andrea adapts herself to this form of mathematical interaction and evaluates the appropriateness of her attitudes. Additionally, she also relies on teacher’s authority to give good explanations (see Appendix 2, Transcript 3).
3. Student’s beliefs about what explaining
why
means and beliefs about mathematics
During the interview, perceptions about what explaining
why
means were studied by analyzing a simple calculation (0.3 x 4 = 1.2) with Andrea. Initially, a simple calculation was selected in order to let Andrea articulate her thoughts and perceptions in a familiar situation. The first step was to look for differences between a
why
question and a
how
one (see Appendix 2, Transcript 4). Secondly, I posed two different written sentences related to this topic (see Appendix 1, Part I, question 2). The first sentence is an algorithm rule often employed by students to explain how to multiply decimals. The second sentence relates decimal notation to decimal fractions, and therefore, multiplying decimals is equivalent to multiplying fractions. That is to say, the second sentence provides a rationale behind decimal numbers’ multiplication. Even though Andrea recognized the validity of both sentence, Andrea never pointed out the need of giving reasons when the teacher asks
why
in mathematics classroom. However, when I asked about why-question in another context, this word appeared (see Appendix 2, Transcript 6).
Andrea perceived checking back with checking numerical computations as essential component of doing mathematics and also suggested that she would prefer to have several methods from which to choose when doing mathematics (see Appendix 2, Transcript 7). Her point of view about mathematics suggests that it is strongly influenced by her beliefs about what doing mathematics means at school as result of her past experiences (see Appendix 2, Transcript 8).
On the basis of the results, I conjecture a simple model of the relationships between the student’s behaviour in a why-situation and her beliefs about mathematics and doing mathematics (see Figure 2).
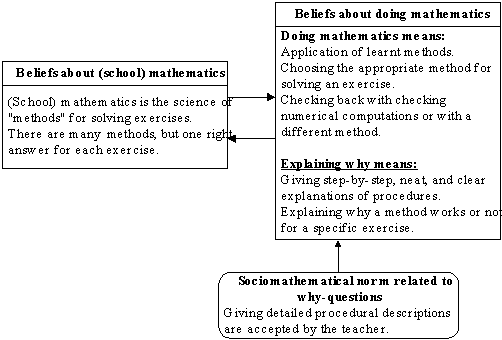
Figure 2 . Hypothetical model of relationships between what explaining why means and beliefs about mathematics and doing mathematics for a student.
Every rectangular shape in the diagram summarizes beliefs about mathematics and doing mathematics inferred during the study. Since the student showed a narrow view about mathematics, beliefs about school mathematics are depicted in the model. The student’s beliefs about what explaining
why
means are included within the set of beliefs about doing mathematics. The arrow pointing from
beliefs about (school) mathematics
to
beliefs about doing mathematics
shows the influence of one on the other, as the review of literature suggests. The opposite arrow denotes that beliefs are acquired through repeated participation in a culture of doing mathematics, as the theoretical review also suggests. Additionally, the hypothetical model illustrates how a particular sociomathematical norm about explaining
why
regulates a specific aspect of the student’s activity.
CONCLUSION
In conclusion, I should give some methodological warnings:
1.
Even though the observed class periods were randomly selected, all of them had the same aim (reviewing learnt topics by checking exercises). I think that another kind of aim, like introducing new topics, would provide different why-situations while students try to understand new material
2.
The discussions about differences between a why-question and a how-question were related to a simple calculation (0.3 x 4 = 1.2). Probably, a more cognitively demanding activity would challenge the student to provide reasons for her thinking and not only procedural explanations, while trying to convince others
3.
Perhaps, discussions about geometrical topics would be more suitable to determine beliefs about explaining in mathematics, since geometry is often presented to students as a context in which justifying, writing arguments, discussing examples and counter-examples are common activities (National Council of Teachers of Mathematics 1987).
Although these considerations would improve the present study, I think that the hypothetical model shows a coherent picture of how beliefs impact on behaviour within a particular activity in mathematics classroom. Consequently, it is suggested that when students are asked to explain their thinking, a how-explanation may be the outcome of their held beliefs about what doing mathematics means and their perceptions of the norms that regulate participation in mathematics classroom.
REFERENCES
Cooney, T., Shealey, B., and Arvold, B. (1998) Conceptualizing belief structures of preservice secondary mathematics teachers, Journal for Research in Mathematics Education , 29 (3), 306-333.
Dossey, J. (1992) The nature of mathematics: its role and its influence, in Grows, D. A. Ed. (1992) Handbook of Research on Mathematics Teaching and Learning , New York: Macmillan, 39-48.
Ernest, P. (1988) The Impact of Beliefs
on the Teaching of Mathematics, web article: http://www.ex.ac.uk/~PErnest/impact.htm
.
Ernest, P. (1994a) Social constructivism and the psychology of mathematics education, in Ernest, P. Ed. (1994)
Constructing Mathematical Knowledge: Epistemology and Mathematical Education
, London: Falmer Press.
Ernest, P. Ed. (1994b) Mathematics, Education and Philosophy: An International Perspective , London: Falmer Press.
Ernest, P. (1996) The nature of mathematics and teaching, Philosophy of Mathematics Education , Newsletter 9 , web article: http://www.ex.ac.uk/~PErnest/pome/pompart7.htm
Ernest, P. (1998) Social Constructivism as a Philosophy of Mathematics , Albany, New York: SUNY Press.
Franke, M. and Carey, D. (1997) Young children’s perceptions of mathematics in problem solving environments, Journal for Research in Mathematics Education , 28 (1), 8-25.
McKernan, J. (1999) Investigación-acción y Curriculum: Métodos y Recursos para Profesionales Reflexivos , Madrid: Ediciones Morata (original in english: McKernan, J. (1996) Curriculum Action Research , London: Kogan Page Limited).
McLeod, D. (1992) Research on affect in mathematics education: a reconceptualization, in Grows, D. A. Ed. (1992) Handbook of Research on Mathematics Teaching and Learning , New York: Macmillan, 575-596.
National Council of Teachers of Mathematics (1987) Resolving the continuing dilemmas in school geometry, Learning and Teaching Geometry, K-12 , 1987 Yearbook , Virginia: NCTM, 17-31.
Raymond, A. (1997) Inconsistency between a beginning elementary school teacher’s mathematics beliefs and teaching practice, Journal for Research in Mathematics Education , 28 (3), 550-576.
Romberg, T. (1992) Perspectives on scholarship and research methods, in Grows, D. A. Ed. (1992) Handbook of Research on Mathematics Teaching and Learning , New York: Macmillan, 49-64.
Sam, L. (2002) Public images of mathematics, Philosophy of Mathematics Education , Journal 15, web article: http://www.ex.ac.uk/~PErnest/pome15/public_images.htm
Schoenfeld, A. (1987) What’s all fuss about metacognition?, in Schoenfeld, A. Ed. (1987)
Cognitive Science and Mathematics Education
, Hillsdale, New Jersey: Lawrence Erlbaum Associates.
Schoenfeld, A. (1992) Learning to think mathematically: problem solving, metacognition, and sense making in mathematics, in Grows, D. A. Ed. (1992)
Handbook of Research on Mathematics Teaching and Learning
, New York: Macmillan, 334-370.
Spangler, D. (1992) Assessing students’ beliefs about mathematics, The Mathematics Educator (on line) 4 (3), 19-23, http://jwilson.coe.uga.edu/DEPT/TME/Issues/v3n1/5spangler.pdf
Thompson, A. (1992) Teachers’ beliefs and conceptions: a synthesis of the research, in Grows, D. A. Ed. (1992) Handbook of Research on Mathematics Teaching and Learning , New York: Macmillan, 127-146.
Wood, T. (1999) Creating a context for argument in mathematics class, Journal for Research in Mathematics Education , 30 (2), 171-191.
Yackel, E. and Cobb, P. (1996) Sociomathematical norms, argumentation, and autonomy in mathematics,
Journal for Research in Mathematics Education
, 27 (4), 458-477.
APPENDIX 1
Semi-structured Interview Questions
I Part
1. Suppose that you have done the calculation: 0.3 x 4 = 1.2, and then, the teacher asks you how do you do it?, or she asks you why does 0.3 x 4 equal 1.2?. Are both questions different or similar? Why?
2. Which explanation of 0.3 x 4 = 1.2 is correct, Sentence 1 or Sentence 2? Are they different?
Sentence 1
: multiply 0.3 and 4 as if both were integers (i.e. 3 x 4 = 12); then, move the dot one place to left in the result (i.e. 1.2) because the only decimal (0.3) has one place after the dot.
Sentence 2
: 3/10 is the fractional notation of 0.3. Then, 0.3 x 4 is the same as 3/10 x 4. Thus, 3/10 x 4 = 12/10. Lastly, 1.2 is the decimal notation of 12/10.
3. Suppose that your teacher have done the calculation 0.3 x 4 = 1.2, and you ask her why 0.3 x 4 equals 1.2. Which sentence (Sentence 1 or Sentence 2) is it supposed that your teacher will use to give you the answer? One of them? Both?
4. Do you sometime ask your teacher why ? In which situations? What is your intention to ask why to your teacher?
5. Do you sometime ask your mum why ? In which situations? What is your intention to ask why to your mum?
II Part
1. Suppose you are working with a partner in your class to solve a math problem and you and your partner get different answers. How do you know which answer is right?
2. When you work to solve a mathematical problem, would you prefer to have one method which works or many methods which work for the problem?
3. Is it possible to get the right answer to a mathematics problem and still not understand the problem?
4. How do you know when you have correctly solved a mathematical problem?
5. Can you think of some characteristic of a partner who is good at mathematics?
6. Do you know that some professionals are mathematicians? What do you think that mathematicians do? Where do they work?
Note
: Original questions were in Spanish.
APPENDIX 2
Transcript 1
Interviewer: Can you think of some characteristic of a partner who is good at mathematics?
Andrea: Well The person must enjoy mathematics and be intelligent.
Interviewer: What does intelligent mean? Describe an intelligent person.
Andrea: This person must understand everything, or almost everything, and make good explanations for the others.
Transcript 2
Interviewer: When your teacher asks you why, what do you think it is a good explanation for her?
Andrea: Well It depends on how I explain. Because if I explain well, step-by-step, she won’t ask me again, but if I do an exercise without explaining well, it will be likely that she goes on asking me.
Transcript 3
Teacher: Your answer is correct, but it’s too intricate. This is more easy (a teacher’s explanation followed)
Andrea: Ah! Yes (while moving her head up-down, quickly gesturing approval to what teacher said)
When the meaning of this situation arose during the interview, Andrea said:
Andrea: Oh! I got into a jam. I had understood the problem but, after the teacher said that, I thought I was wrong. I got confused!
Transcript 4
Interviewer: If the teacher asks you How did you do 0.3 x 4?, what do you answer?
Andrea: I must answer how I have got , how I have to do to get the result.
Interviewer: And if the teacher asks you Why does 0.3 x 4 equal 1.2?
Andrea: Well, I must answer why, why I have to use this method to get the result.
Transcript 5
Andrea: Oh! Well, the procedure is different, but by using either of the two, we get the same result.
When asked if a teacher ought to give both explanation to his/her students, Andrea said:
Andrea: Yes. Because , it’s likely that this (pointie one (an exercise), I can use this (pointing at the first sentence), but if there are more fractions, this one (pointing at the second sentence) will be convenient.
Transcript 6
Interviewer: Do you sometime ask your mum
why
?
Andrea: No! (I realized that she was thinking about mathematics)
Interviewer: And what about if your mum don’t let you go out dancing with your friends? Do you ask her why ?
Andrea: Yes! (laughingly)
Interviewer: Why do you ask
why
to your mum in this situation?
Andrea: Because if she doesn’t let me go out, she ought to have a good reason!
Transcript 7
Interviewer: When you work to solve a mathematical problem, would you prefer to have one method which works or many methods which work for the problem?
Andrea: Many methods.
Interviewer: Why?
Andrea: Because if I have one (method) well, I apply it and obtain a result. Then, I check it back and I ought to obtain the same result. But, if I have many methods, I apply them to see if I obtain the same result.
Transcript 8
Interviewer: Do you know that some professionals are mathematicians?
Andrea: No.
Interviewer: No? Don’t you imagine what a mathematician does?
Andrea: . figuring out procedures to solve exercises!
ACKNOWLEDGMENT
I am very grateful to the host school, for the extraordinary support of the school principal, of the 1st year classroom teacher, and of her students.